Preface by the author
最近在复习ML时看到一篇五年前的CNN文章(这位印度小哥后续的博客也相当attractive),作者写的相当深入浅出,所以本人特意准备以此为baseline来描述一下个人对于NN的理解。关于 Convolutional Neural Networks, 本人有幸在CUHK选修过Prof. Hongsheng(今年爆火的几篇Transformer也有李老师的参与)的 ML for SP Applications 。虽然最后‘喜提’B+(别问,问就是人菜瘾大 😧),但是这门课对于我最后的research thesis相当有用。但是因为本人的tech stack偏向于IoT和embedded systems,数学功底不扎实。如有谬论,敬请指正(暂未集成评论功能,欢迎通过GitHub的issue来评论,唔该!)。
Disclaimer
由于该文章主要是用于本人的学习总结和复习,所以行文风格略为洒脱。另外,本人思维较为发散,如果你发现文章中经常乱入其他内容的知识,敬请谅解 😎
Abstract
Convolutional neural networks 听起来像是神经科学的一个专业名词,但它其实是一个AI中的重要部分(即使无较大关联,但是NN对于研究人类的学习模式有很重要的启发作用,可以参考这两个文章:人脑是怎么防止梯度消失和梯度爆炸的, 详解深度学习中的梯度)。它可以追溯到上世纪中期(具体时间忘记了),但到了2012年的时候,在ImageNet的比赛中才崭露头角。从此之后,多种魔改的NN模型层出不穷,如ResNet等。它们大部分是通过修改网络的结构和组成部分(如激活函数,Loss function等)来追求SOTA。因此,如果新人可以先对一个基本的NN了解的话,那么也能大致清楚DL为什么workable。
Introduction
在作者看来,智慧物种本身就是一群掌握了一定 学习->应用 能力的生物,包括人类。在丛林中,食肉动物会通过观察猎物的外形特征来判断是否可以将其作为捕猎对象。在城市里,人们饲养的宠物多数时间可以通过主人的情绪表现出不同的行为。而人类在数千万年间的进化中,凭借出色的 学习 (ability to be trained) 能力逐渐成为了万物的领跑者。因此,深度学习理论并未被提出的亿万年间,其雏形便隐隐发挥着不小的作用。而随着对人类神经科学的探索,研究人员们已经逐渐理清人类的学习模式与AI之间的共通之处。
Methods
以人类为例,当一个可以正常思考的人来判断站在他面前的是鸟还是狗时,他可以通过被观察对象的特征来进行判断。例如,这个对象是否有爪子,是否有翅膀,是否有尾巴等。事实上,CNN模型在进行这样的分类判断(即classification)时,也可以通过这样的 特征 来进行分类。但在processing中,它会将人眼可见的high-level信息转为low-level再进行判断(图像中语义信息、高层和底层特征)。而由于0和1组成了计算机的底层运算逻辑,所以运行在计算机上的模型所看到的,也是由多个数字矩阵所组成的一张图片。例如对于一张分辨率为 256 x 256 的图片,DL算法会将其当作是一个 256 * 256 * 3 的矩阵(这个3是因为RGB图像由三种颜色组成)。因此,CNN模型的初始input一般来说就是一个相似的矩阵。
在DL中,一个CNN是由很多layers组成,可以大致分为convolutional, nonlinear, pooling (downsampling/subsampling,用以缩小feature map。上,下采样可以看这里,而pooling就是subsample的一种), 和fully connected layers。经过fully connected后,模型通常会输出一个多分类的1*N的矩阵(N为分类数),而该矩阵的每个元素相当于输入对象属于某一分类的probability。
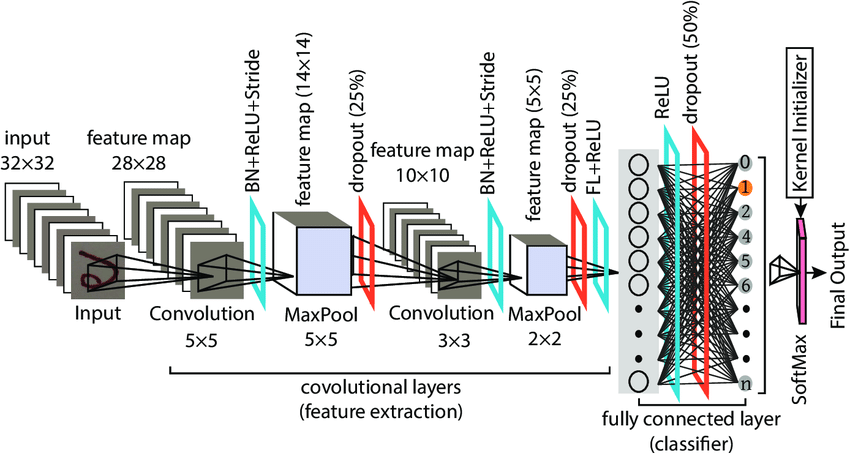
First layer: Conv
经过预处理的有着规定大小的data传入CNN中时,它们要经历的第一道关卡便是 convolutional layer 。卷积层(也作filter或kernel)的概念源自于信号处理中的卷积运算,因为研究人员发现了其 特征抽取 的特性后,将其应用在神经网络中来获得feature map。它的基本运算法则是:在设置好hyperparameters(例如stride,padding等)后,对应的元素相乘后累加,最后获得一个数。事实上,如果将filter具象化,我们可以很轻易地看出,输出的这个数可以表示filter对应的特征采样部分所检测到的图像信息。在下面的例子中,input是一个 5 * 5 的二维矩阵(实际上输入常常是 N * N * 3 ),那么我们可以使用一个 3 * 3 的filter来进行采样,具体的处理过程可以参考下面的动图。而在实际应用时,CNN的conv layer往往有多个filter,以此来获得压缩后的尽可能多的输入信息。
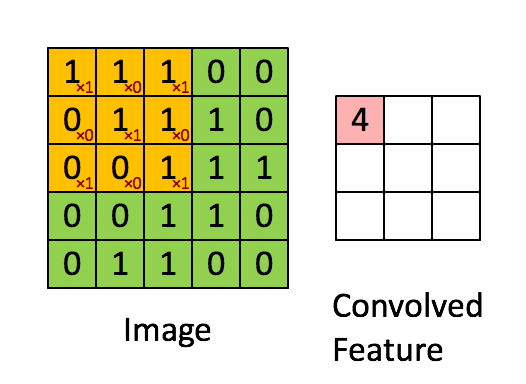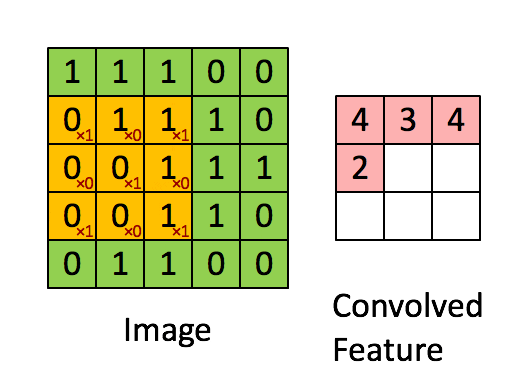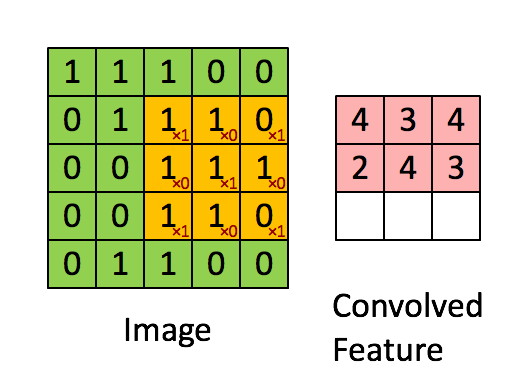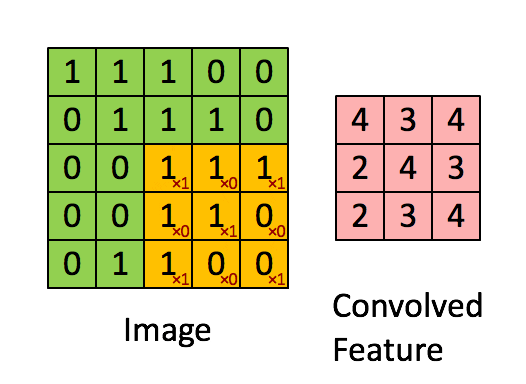
笔者在最开始理解CNN的时候只是单纯地从Linear Algebra的角度来理解,即把conv layer的操作当作是矩阵间的运算来获得feature map。事实上,我们也可以将filter具象化( 矩阵->图像 )来更直接地理解它为什么workable。如下图这个简化的例子,如果我们将这个 7 * 7 的filter可视化后,会发现这是一条曲线。当使用这个filter去进行卷积操作时,越是与其有交集的图片,conv layer’s output就相对越大。相反的是,越是与其没有交集的图片,它的output就会越小,这也是为什么一个conv layer通常会需要多个filter的原因(来提取尽可能多的feature)。这就是上述的 特征抽取 的原理。因此,我们可以更清晰地理解卷积层的作用。而随着卷积层的增加(go deeper),因为feature map的逐渐精简,后面的filter会有越来越大的receptive field for the original input volume(They are more responsive to a larger region of pixel space)。这也是NN一个有趣的地方
![]()
Last layer: Fully Connected Layer
我们先省略从first layer到last layer中间的nonlinear and pooling layers,直接来看最简单的Fully Connected Layer(因为对他们的介绍会耗费大量的时间,笔者先从最容易理解或者帮助新手入门的角度来写)。FC通常是NN的 特征抽取 的最后一层,它的input通常是一个一维向量(不管这个向量是由上一层的conv,pooling还是ReLU输出的),而FC’s output通过softmax (kernel initializer) 后会是一个1*N的矩阵(N为分类数)。举个例子,对于一个输出目标为10分类(如CIFAR10)的model来说,FC的输出可以是[0 .1 .1 .75 0 0 0 0 0 .05],就代表属于a0的可能性是0,a1的可能性是0.1,以此类推。由此可见,FC的工作方式是检查上一层输出的feature map,并决定哪些特征对应于具体的class。如上所述,如果该feature map来自于dog类,那么它里面肯定有有一个较高的值来表示四条腿或者dog face。

